Certain problems can be solved quite easily using recursion. It is the process in which a function calls itself directly or indirectly by defining a base case. Sometimes, using recursion can be a bit complicated, like if the base case is not reached or not defined, which can be very slow.
Memoization is a very effective technique that accelerates recursion. So what is memoization ? And how does it work ?

1. Overview

Let $f$ be a function. Memoizing $f$ is switching between the calls of $f$ and checking whether the value of an input $x$ can already be found in the memory whenever $f(x)$ is to be computed. If $x$ is not already present in the memory, we compute $f(x)$ using its recursive definition and store the resulting value in it.

Memoization is similar to a very familiar technique we already know in computer science, caching ! The aim goal of caching techniques is avoid doing the same thing repeatedly to avoid spending unnecessary running time or resources.

To understand how the memoization works and why is it effective, let’s take a small and simple example. First, we will introduce a naive solution then try to optimize it using memoization.

2. Memoization in example - Fibonacci sequence

Let’s take the Fibonacci sequence, which defines every number after the first two as the sum of the two preceding ones. Its recurrence relation is defined as :

\[\begin{equation} F(n) = F(n-1) + F(n-2) \end{equation} \label{eq:fibo}\]

where seed values are,

\[\begin{cases} F(0) = 0, \\ F(1) = 1. \end{cases}\]

To calculate the Fibonacci sequence defined in \eqref{eq:fibo}, we can use an iterative or a recursive version. Beside the disadvantages of recursion (slow), its main advantage is making the algorithm a little easier and more readable.

def fibo_iterative(n: int):
	"""
	Iterative version of Fibonacci sequence
	"""
	assert n >= 0, "shouldn't be a negative number."
	n2, n1 = 0, 1 # seed values are 0 and 1
	for i in range(n):
		n2, n1 = n1, n2 + n1
	return n2


def fibo_recursive(n: int):
	"""
	Recursive version of Fibonacci sequence
	"""
	assert n >= 0, "shouldn't be a negative number."
	if n < 2: # seed values, if n equals 0 or 1
		return n
	else:
		return fibo_recursive(n-1) + fibo_recursive(n-2)

After running these two functions on few examples, we will notice that the recursive version takes more time than the iterative form which is instant when $n$ grows up.

Why the recursive form takes much more time ? To answer that, we need to understand how it’s calculated.

Figure 1 - The Fibonacci sequence.

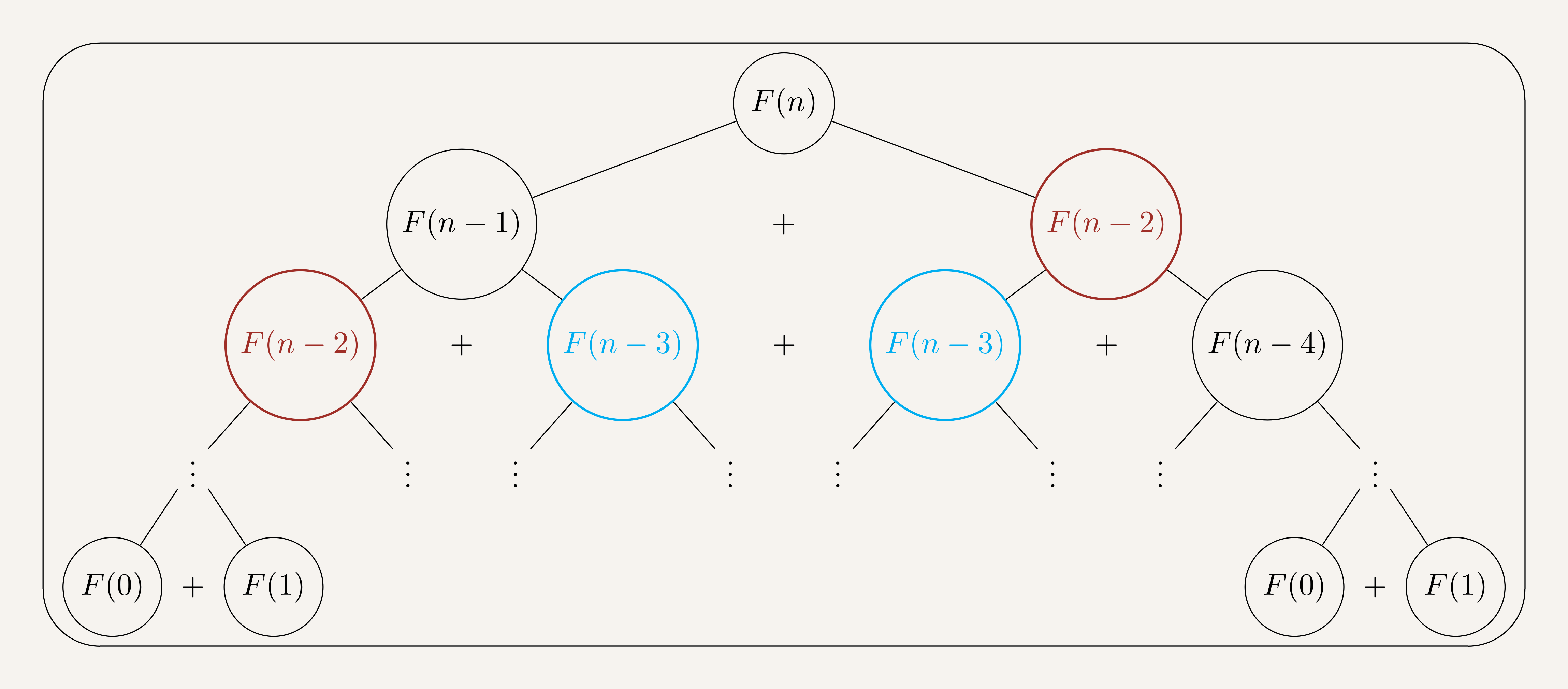
The Figure 1 describes how the recursive form works when trying to compute $F(n)$. By defintion (cf. \eqref{eq:fibo}), calculating $F(n)$ refers to calculating $F(n-1)$ and $F(n-2)$. Let’s focus on $F(n-2)$ (red circles), its calculation requires the calculation of $F(n-3)$ (blue circles) and $F(n-4)$.
We notice that the calculation of $F(n-2)$ is done twice (or more), as well as $F(n-3)$ and every other element in the sequence (except for $F(n-1)$). This redundancy is the principal reason of the long execution time of recursion. To resolve that, we use memoization.

The main goal of memoization in our example is calculating every element in the tree exactly once. To ensure that, at each calculation step we check if we already calculated the input, if yes we check the saved list of calculated inputs, else we calculate it. To store the calculation results, we can use a simple dictionary that gives us a fast search while looking for every element.

3. Speed isn’t everything

Memoization technique is very powerful, it allows us to keep the code readability and being fast at the same time. But this fast execution time costs us another resource, memory.
The data structure choice for saving the intermediate results is important. For example, choosing a dictionary structure is very fast ¹ while it consumes a lot of memory.

In Python, we have a built-in function for memoization that we can find in functools module with the name lru_cache(). This function is a high-order function that can be used as a decorator.

4. Conclusion

Memoization is a very powerful technique to optimize our execution time, but still we need to be careful while using it. We can limit the memory cost for an acceptable running time. This technique opens the topic to many other fields, for example Dynamic Programming which is an algorithmic technique for solving an optimization problem.

1. In base cases when the hash function is perfect, the time complexity is equal to $\mathcal{O}(1)$. ↩