One of the most well known problems in graph theory is the four color theorem for map coloring. A simple example to understand that problem is, given a geographical map, how many colors are required to color it so that no two adjacent regions have the same color ? The answer is four, but it took a long time to prove this theorem after many false proofs and counterexamples.
This problem led to the development of useful tools for graphs coloring as Chromatic polynomials and Chromatic number. The graph coloring problem has a huge number of applications : making schedule or time table, register allocation, mobile radio frequency assignement\(\dots\)

1. Introduction

Let $G(V(G), E(G))$ be a graph and $\lambda \in \Bbb{N}^* $, where $V(G)$ and $E(G)$ are respectively the vertex set and the edge set of $G$.

We call a proper $\lambda$-coloring, a function \(ƒ : V(G) \rightarrow \{1, 2, \dots, \lambda\}\), where for each $u, v \in V(G)$ we have $ƒ(u) \neq ƒ(v)$ whenever $u$ and \(v\) are two adjacent vertices in $G$. We say that two $\lambda$-colorings $ƒ$ and $g$ are distincts, if for some vertex $x$ of $G$, $ƒ(x) \neq g(x)$. Which means that given $\lambda$ colors, we need to find a way of coloring the vertices of $G$ such that no two adjacent vertices are colored using the same color.

There are several ways to color $G$ in $\lambda$-coloring, the number of distinct ways is denoted by $P(G, \lambda)$ and called the chromatic polynomial (Birkhoff, 1912). By interpreting $\lambda$ as the number of colors, we can never color a graph with zero colors which will give us $P(G, \lambda)$ is not $\lambda$-colorable. By definition, we say that $G$ is $\lambda$-colorable if and only if $P(G, \lambda) \geq 1$, since it exists at least one way of $\lambda$-coloring.

Among the most classic problems in graph theory is to find the minimum number of colors to color the graph $G$. This number is called the chromatic number and is denoted by $\chi(G)$.

\[\begin{equation} \chi(G) = \min\{\lambda \in \Bbb{N}^* : P(G, \lambda) \geq 1 \label{eq:chrom_num}\} \end{equation}\]

By definition, $P(G, \chi(G)) \geq 1$ ¹. Given a set of $r$ colors ($r \in \Bbb{N}$), for $r < \chi(G)$, $P(G, r) = 0$.

2. Particular graphs

After having defined the graph coloring, we will try to enumerate $P(G, \lambda)$ for some special graphs.

2.1. Examples

For an empty graph $O_n$ of order $n$, it is clear that, $$ \begin{equation} P(O_n, \lambda) = \lambda^{n} \end{equation} $$ More generally, when $G$ contains $k$ connected components, we have $G = \bigcup_{i=1}^{k} G_i$, then $$ \begin{equation} P(G, \lambda) = \prod_{i=1}^{k} P(G_i, \lambda) \end{equation}$$

For a complete graph $K_n$ of order $n$ where $\forall u, v \in V(G)$ they are adjacents (by definition $ƒ(u) \neq ƒ(v)$), we have $$ \begin{equation} P(K_n, \lambda) = \lambda(\lambda - 1)\dots(\lambda - n +1) \end{equation} \label{eq:complete_graph} $$

Figure 1 - A complete graph of order 5.

Let $H$ be a graph containing a $K_r$ as subgraph, and let $G$ be the graph obtained from $H$ by adding a new vertex $w$ which is linked with each vertex in $K_r$, then $$ \begin{equation} P(G, \lambda) = (\lambda - r)P(H, \lambda) \end{equation} $$

Let us compute $P(C_4, \lambda)$, where $C_4$ is a cycle graph of order 4.

Figure 2 - A cycle graph of order 4.

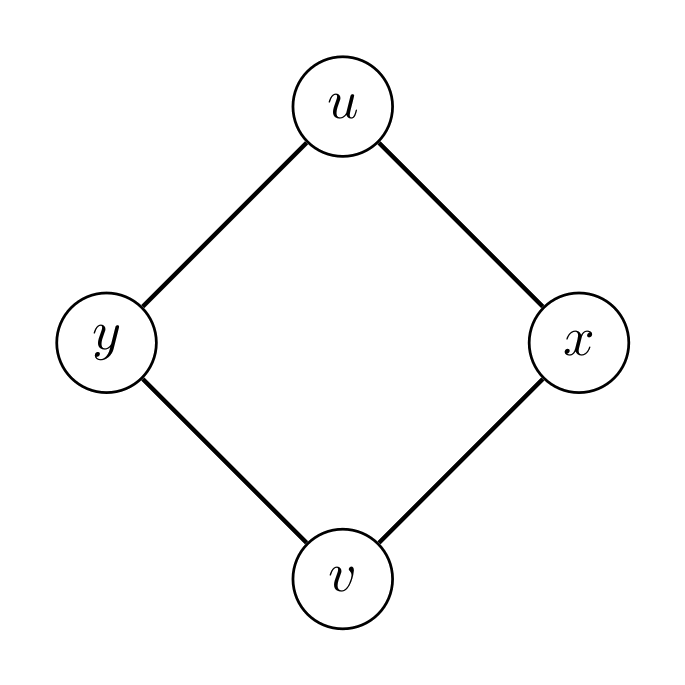
Let $ƒ$ be a $\lambda$-coloring of $C_4$ and $u, v$ two non adjacent vertices, we enumerate two cases,

1. $ƒ(x) = f(y)$. There are $\lambda - 1$ ways to color the vertices $u$ and $v$ independently, so the number of $\lambda$-colorations is $\lambda (\lambda - 1)^2$,
2. $ƒ(x) \neq f(y)$. There are $\lambda - 2$ ways to color the vertices $u$ and $v$ independently, so the number of $\lambda$-colorations is $\lambda (\lambda - 1) (\lambda - 2)^2$.

We conclude that,

\[\begin{equation}\begin{aligned} P(C_4, \lambda) &= \lambda (\lambda - 1)^2 + \lambda (\lambda - 1) (\lambda - 2)^2 \\ &= \lambda^4 - 4 \lambda^3 + 6 \lambda^2 - 3 \lambda \\ &= (\lambda - 1)^4 + (\lambda - 1) \end{aligned}\end{equation}\]

2.2. Stirling numbers of the first kind

From equation \eqref{eq:complete_graph}, we observe that,

\[\begin{equation*}\begin{aligned} P(K_1, \lambda) &= \lambda \\ P(K_2, \lambda) &= \lambda (\lambda - 1) = \lambda^2 - \lambda \\ P(K_3, \lambda) &= \lambda (\lambda - 1) (\lambda - 2) = \lambda^3 - 3 \lambda^2 + 2 \lambda \\ & \vdots \end{aligned}\end{equation*}\]

Generally, when $P(K_n, \lambda)$ is expressed in terms of powers of $\lambda$, we have

\[\begin{equation} P(K_n, \lambda) = \lambda (\lambda - 1) \dots (\lambda - n + 1) = \sum_{k=1}^n \mathcal{s}(n, k) \lambda^k \end{equation}\]

Where $\mathcal{s}(n, k)$ are the Stirling numbers of the first kind, which are defined as

\[\begin{equation} \mathcal{s}(n, k) = \mathcal{s}(n - 1, k - 1) - (n - 1) \mathcal{s}(n - 1, k) \end{equation}\]

where,

\[\begin{cases} \mathcal{s}(r, 0) = 0, \;\; \forall r \in \Bbb{N^* }, \\ \mathcal{s}(r, r) = 1, \;\; \forall r \in \Bbb{N} \end{cases}\]

3. Calculation of the chromatic polynomial

The problem to find $\chi(G)$ of a given graph is NP-Complete, and the problem to evaluate $P(G, \lambda)$ is as hard as finding the $\chi(G)$. Despite this, the calculation of $P(G, \lambda)$ gives us a lot of important information about graphs, which it attracts more attention by researchers. We will introduce some important results about $P(G, \lambda)$ computation for some classes of graphs. (Dong et al., 2005)

First, we will use an extension of the idea used for the computation of $P(C_4, \lambda)$ that we will use for $P(G, \lambda)$ computation.

Let $x$ and $y$ be two non-adjacent vertices in a graph $G$, then $$ \begin{equation} P(G, \lambda) = P(G + xy, \lambda) + P(G \cdot xy, \lambda) \label{eq:calculus} \end{equation} $$ Proof.   Let $ƒ$ be a $\lambda$-coloration of the graph $G$. We have either (i) $ƒ(x) \ne ƒ(y)$ or (ii) $ƒ(x) = f(y)$. The number of $\lambda$-colorings $ƒ$ of $G$ for which (i) holds equals $P(G + xy, \lambda)$, while the number of $\lambda$-colorings $ƒ$ of $G$ for which (ii) holds equals $P(G . xy, \lambda)$.

$\square$

Let $G$ be the following graph,

Figure 3 - A graph $G$ of order 5.

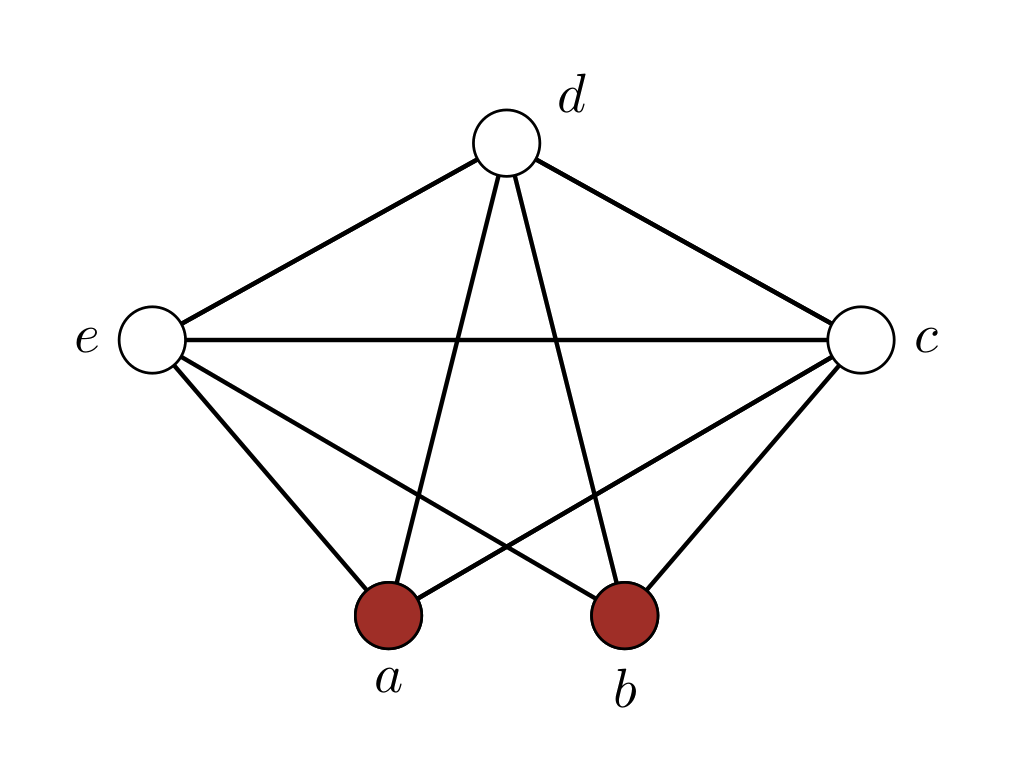
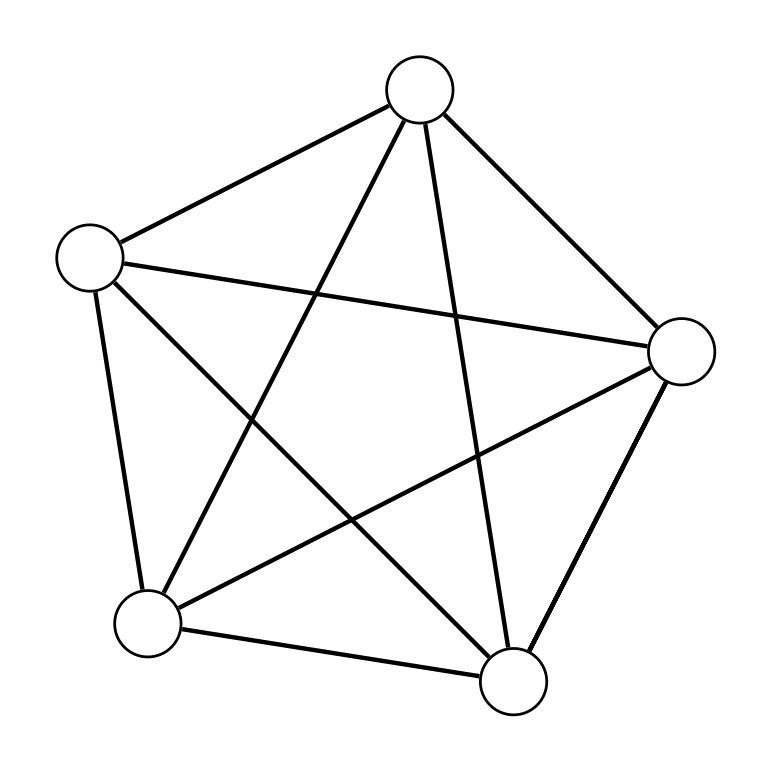
By applying \eqref{eq:calculus}, we get 2 graphs :

• $G + ab$, the graph obtained by adding a new edge $ab$ to $G$, which is a complete graph of order 5,
• $G \cdot ab$, the graph obtained from $G$ by contracting $a$ and $b$ and removing any loop, which is a complete graph of order 4.

Thus,

\[\begin{equation*}\begin{aligned} P(G, \lambda) &= P(K_5, \lambda) + P(K_4, \lambda) \\ &= \lambda (\lambda - 1) (\lambda - 2) (\lambda - 3) (\lambda - 4) + \lambda (\lambda - 1) (\lambda - 2) (\lambda - 3)\\ &= \lambda^5 - 9 \lambda^4 + 29 \lambda^3 - 39 \lambda^2 + 18 \lambda \end{aligned}\end{equation*}\]

Chromatic polynomials are a very useful tools for graphs, they are applied in many fields. As a simple example, we will try to apply it to a very famous game, Sudoku.

4. Behind the Sudoku

Sudoku is a puzzle that has become very popular. The game consists of a grid of 9 $\times$ 9 where each box contains a number from 1 to 9. One must fill the grid in a way where each row, each column and each sub grid contain numbers from 1 to 9 exactly once.

A Latin square of order $n$ is a grid of size $n \times n$ where each row and each column contain all the numbers between 1 and $n$ repeating exactly once. Each Sudoku grid is a Latin square of order 9, but the converse is not true because of the condition of the sub grids.

After understanding the principle of the game, we will approach to see a Sudoku grid using graphs (Herzberg & Murty, 2007). We can see the Sudoku grid as a coloring problem. In fact, by associating to each grid a graph of order 81 (9 $\times$ 9), where each vertex corresponds to a cell in the grid. Two distincts vertices are adjacent if and only if the two corresponding cells in the grid are either in the same row, same column or same sub grid.
Each Sudoku solution corresponds to coloring the associated graph. We can generalize this by considering a grid of size $n^2 \times n^2$. For each cell of the grid we associate a vertex denoted by $(i, j)$, with $1 \leq i, j \leq n^2$. We say that $(i, j)$ and $(i’, j’)$ are adjacents if $i = i’$ or $j = j’$ or $\lceil i/n \rceil = \lceil i’/n \rceil$ and $\lceil j/n \rceil = \lceil j’/n \rceil$ where $\lceil \,. \rceil$ denotes the ceiling function.

Let $X_n$ be a graph that we call a Sudoku graph of order $n$. It’s clear that $X_n$ is a regular graph ² such that each vertex is of degree $3n^2 - 2n - 1 = (3n + 1)(n - 1)$. In particular, $X_3$ graph corresponds to a 9 $\times$ 9 grid that is a 20-regular graph.

References

1. Birkhoff, G. D. (1912). A Determinant Formula for the Number of Ways of Coloring a Map. Annals of Mathematics, 14(1/4), pp. 42–46.
   @article{birkhoff12,
     added-at = {2015-05-10T13:10:32.000+0200},
     author = {Birkhoff, George D.},
     issn = {0003486X},
     journal = {Annals of Mathematics},
     keywords = {},
     language = {English},
     number = {1/4},
     pages = {pp. 42-46},
     privnote = {Birkhoff's original definition of chromatic polynomials},
     publisher = {Annals of Mathematics},
     series = {Second Series},
     title = {A Determinant Formula for the Number of Ways of Coloring a Map},
     volume = {14},
     year = {1912}
   }
   

2. Dong, F. M., Koh, K. M., & Teo, K. L. (2005). Chromatic Polynomials and Chromaticity of Graphs.
   @book{Dong2005,
     author = {Dong, F. M. and Koh, K. M. and Teo, K. L.},
     title = {{Chromatic Polynomials and Chromaticity of Graphs}},
     year = {2005}
   }
   

3. Herzberg, A. M., & Murty, M. R. (2007). Sudoku Squares and Chromatic Polynomials. Notices of the AMS, 54(6), 708–717.
   @article{Herzberg2007,
     author = {Herzberg, Agnes M and Murty, M Ram},
     journal = {Notices of the AMS},
     number = {6},
     pages = {708--717},
     title = {{Sudoku Squares and Chromatic Polynomials}},
     volume = {54},
     year = {2007}
   }
   

1. $G$ is $\chi(G)$-colorable. ↩

2. A regular graph is a graph where each vertex has the same degree; i.e. has the same number of neighbors. ↩